3角形分割の何がおもしろいか?
点配置を与えられたとき、それらの点のみを使った、その凸包の3角形分割
(triangulation)は何通りかある。例えば、凸5角形の頂点の点配置について
は、図の5つの3角形分割がある。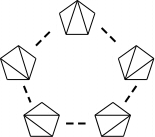 3角形分割全体は、ただあるだけではなく、その中に構造を持っている。例え
ば、先程の凸5角形の例では、辺を一つだけ入れ替えることによって移り変わ
れる(この操作は flip とよばれている)3角形分割が、図の中で点線で結ばれ
ている。このような局所的な変更のみで移りあえるという関係について、5つ
の3角形分割は5角形の形をしたグラフの構造を持っていると言える。
一般次元において、3角形分割全体がどのような構造を持つかを解明するのが
われわれの研究の目的である。
3角形分割全体は、ただあるだけではなく、その中に構造を持っている。例え
ば、先程の凸5角形の例では、辺を一つだけ入れ替えることによって移り変わ
れる(この操作は flip とよばれている)3角形分割が、図の中で点線で結ばれ
ている。このような局所的な変更のみで移りあえるという関係について、5つ
の3角形分割は5角形の形をしたグラフの構造を持っていると言える。
一般次元において、3角形分割全体がどのような構造を持つかを解明するのが
われわれの研究の目的である。
これまでの研究成果(論文)
- 3角形分割の列挙
現在までの研究では、3角形分割全体を効率的に列挙する手法を確立した。ま
た、実際にこのアルゴリズムを実行するプログラムを作成した。3角形分割の
様子が、数学的に興味深いような点配置は、対称性のある点配置であることが
多い。このような対称性のある点配置について、正則な3角形分割を効率的に
列挙する手法も開発した。
- 3角形分割と3角形分解の関係
3角形分割においては、分割の結果の各部分がきれいに接していることが求め
られる。しかし、体積計算など一部の応用では、切り分けられれば十分であり、
接し方までは要求されない(このようなものを3角形分解 simplicial
decomposition とよぶ)。この2つのクラスの違いについて、最小3角形分解が
最小3角形分割よりも少ない数の単体で済む例、最大3角形分解が最大3角形分
割よりも多くの単体を必要とする例、3角形分解における上限定理や下限定理
などを示した。
- 単体的複体の逐次的分解についての性質
3角形分割はより広く、単体的複体というクラスに属する。単体的複体の逐次
的な分解のしやすさについて、いくつかの性質が知られている。これらの性質
の間の関係を明らかにした。コンピュータで幾何的なものを扱うとき、このよ
うな逐次的な処理の可能性を考えることは大切である。
3角形分割の応用
凸多面体を扱うとき、それをより小さなものに分割することによって、より上
手く扱えることは多い。3次元の点配置を扱う分野では3角形分割も必要になり、
それらの分野は、立体の表示を扱う3次元コンピュータ・グラフィックス、シュ
ミレーションにより計算を行う工学、DNAの立体構造を扱う生物学など数多い。
ホームにもどる
 Last modified: Wed Jan 5 20:31:22 2005
Last modified: Wed Jan 5 20:31:22 2005
 Last modified: Wed Jan 5 20:31:22 2005
Last modified: Wed Jan 5 20:31:22 2005